Steps:
- Determine the types of data
- Determine the number of samples
- If two samples: are they independent groups or related (matched) groups?
- Choose the test
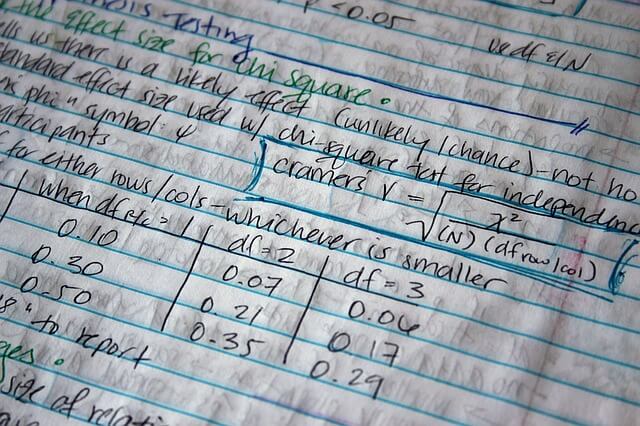
Types of data
Mnemonic: NOIR
Qualitative or Categorical data
a. Nominal (relating to name): Groups e.g. gender (male/female), color (black/white), blood groups (A/B/AB/O), religions (hindu/muslim/christian)
b. Ordinal (relating to order): Rank-ordered data but without meaningful difference; e.g. socio-economic status (low, middle and high), rank (1st, 2nd and 3rd)
– without meaningful difference: difference between 1st and 2nd may be 20 units but that between 2nd and 3rd may be only 3 units
Quantitative or Numerical data (Scale)
a. Interval (means gap): values can be ordered and have a meaningful difference but doubling is not meaningful because there is no “true zero” point
– with meaningful difference: difference between 100 and 90 celsius is same as that between 50 and 40 celsius, i.e. 10 celsius
– without meaningul doubling: 100 celsius is not twice as hot as 50 celsius because 0 celsius doesn’t indicate complete absence of heat
b. Ratio: Similar to interval data but with meaningful doubling because it has “true zero” point (0 means absence of something)
– with meaningful doubling: weight (100 kg is twice as heavy as 50 kg), height (100 cm is twice as tall as 50 cm), kelvin scale (300K is twice as hot as 150K), blood pressure (120 mmHg is twice as high as 60 mmHg), pulse rate (120 beats/min is twice as high as 60 beats/min)
Quantitatve data can also be:
1. Discrete: Only integers (no fraction or decimals); e.g. number of people (178 or 179; 178.5 is not possible)
2. Continuous: Fractions or decimals possible; e.g. temperature (100.4 F), weight (65.7 kg)
Summary: NOIR
- Nominal: groups
- Ordinal: ordered ranks
- Interval: meaningful ordered difference but no meaningul doubling (no true 0 point)
- Ratio: meaningful ordered difference with meaningul doubling (true 0 point)
- Discrete: integers only
- Continuous: fractions or decimals possible
- Independent variable: Investigator manipulated variable (input)
- Dependent variable: Measured variable (output)
Plotting a histogram or QQ plot of the variable of interest will give an indication of the shape of the distribution. Histograms should peak in the middle and be approximately symmetrical about the mean. If data is normally distribued, the points in QQ plots will be close to the line.
Tests of statistical significance and association
| Parametric tests | Non-parametric tests | |
| Based on | Normal distribution | Non-normal distribution |
| Types of data | Quantitative | Qualitative |
| Compares | Means (+SD) | Percentage, proportions and fractions |
| Examples | Students (paired) t-test Students (unpaired) t-test ANOVA (F test) | Sign test Chi-square test Wilcoxan test Mann-Whitney test |
| Comparing: | Dependent variable | Independent variable | Parametric test (Dependent variable is normally distributed) | Non-parametric test |
| Means of 2 independent groups | Continuous/Scale | Categorical/nominal | Unpaired t-test z test (if sample >30) | Mann-Whitney U test or Wilcoxon (rank sum) test if data atleast ordinal |
| Means of 2 paired (matched) groups | Continuous/Scale | Time variable (Time 1 = before, Time 2 = after) | Paired t-test | Sign test or Wilcoxon signed rank test |
| Means of 3+ independent groups | Continuous/Scale | Categorical/nominal | ANOVA | Kruskal-Wallis test |
| 3+ measurment on the same subjects | Continuous/Scale | Time variable | Repeated measures ANOVA | Friedman test |
| Relationship between 2 continuous variables | Continuous/Scale | Continuous/Scale | Pearson’s correlation coffecient (r) | Spearman’s correlation coffecient (rho) – also used for ordinal data |
| Predicting the change in dependent variable with the change in independent variable | Continuous/Scale | Any | Simple linear regression (1 independent variable) Multiple linear regression (2 or more independent variables) | |
| Qualitative | Any | Logistic regression | ||
| Relation between 2 categorical variables | Categroical/nominal | Categorical/nominal | Chi-square test Fischer’s test (if sample size <30) |
When analyzing the relation between 2 nominal variables, create a 2X2 contingency table. Calculate the expected value (E) for each of the 4 cells. If E is <5, use Fischer’s test and if E is >/= 5, use Chi-square test. Fischer test is more accurate for smaller sample size and Chi-square test is more accurate for larger sample size.
Expected value can be calculated for a cell by multiplying total of the row and total of the column corresponding to that cell and dividing by grand total.
Examples:
a. Is diet A better than diet B for weight loss?
- 1 nominal: Diet A or B
- 1 scale: Weight loss (dependent variable)
Choice of test: Normal distribution – unpaired t test; Non-normal distribution – Mann whitney U test or Wilcoxan (rank sum) test
b. Are height and weight related?
- 1 scale: Height
- 1 scale: Weight
Choice of test: Normal distribution – Pearson’s correlation coefficient; Non-normal distribtion – Spearman’s correlation coefficient
c. Can height predict weight?
- 1 scale: Height
- 1 scale: Weight (dependent variable)
Choice of test: Simple linear regression
d. Are patients taking treatment A more likely to recover than those taking treatment B?
- 1 nominal: treatment A or B
- 1 nominal: early recovery or late recovery
Choice of test: Chi-square test
e. 30% of students in a class are anemic, after 6 months of IFA therapy, now 20% of students are anemic – how do you test the significance?
- 1 scale: percentage of anemic
- 1 time interval: before 6 months and after 6 months (matched group)
Choice of test: Sign test or Wilcoxon (signed rank) test (percentage = non-parametric)
f. Mean serum albumin level of dengue patients before treatment was 3.6 gm/dl and after treatment was 3.2 gm/dl.
- 1 scale: albumin level
- 1 time interval: before treatment and after treatment (matched group)
Choice of test: paired t-test (mean = parametric)
g. Mean Hb level of anemia patients was 9.6 gm/dl and those of hookworm patients was 7.2 gm/dl.
- 1 scale: Hb level
- 1 nominal: Anemia patients or hookworm patients
Choice of test: unpaired t-test (if sample <30) or z test (if sample >30)
h. Mean weight of students in class A is 50 kg, class B is 44 kg and class C is 52 kg.
- 1 nominal: 3 groups (Class A, B and C)
- 1 scale: weight
Choice of test: 1 way ANOVA
i. A doctor believes that drawing blood is faster with a vacutioner for someone once that person is trained, but faster with a standard syringe for someone with no training.
- 1 scale: time (faster vs slower)
- 1 nominal: vacutioner or syringe
- 1 nominal: trained or non-trained
Choice of test: 2 way ANOVA
j. Do body weight, calorie intake, fat intake, and age have an influence on the probability of having a heart attack?
- Dependent variable: nominal (influence probability of having heart attack – yes or no)
- Independent variables: Body weight (scale), Calorie intake (scale), Fat intake (scale)
Choice of test: Logistic regression
Interpretation of the test
| Inferential statistics test | Rules for significance (Null hypothesis rejected) |
| Spearman’ Rank | Calculated rho =/> critical value |
| Chi-Square | Calculated X² =/> critical value |
| t-test | Calculated t =/> critical value |
| Sign Test | Calculated S =/< critical value |
| Wilcoxon | Calculate T =/< critical value |
| Mann-Whitney | Calculated U =/< critical value |
Some addition information
a. Applications of chi-square test:
- Test of proportions
- Test of association
- Test of goodness of fit (for single data)
b. Essential requirements for calculation of chi-square test:
- Random sample
- Qualitative data
- Lowest expected frequency not <5
c. Degrees of freedom: It is the number of observations in a dataset that can freely vary once the parameters have been estimated. It is used in chi-square test and t-test. It is calculated as:
- Single sample (paired t-test): n-1 (where n is the no. of units in the sample)
- Two sample (unpaired t-test): (N1 + N2) – 2; where N1 and N2 is the no. of units in the two samples)
- Chi-square test, contingency table: (c-1)(r-1); where c is no. of columns and r is no. of rows
d. Correlation is represented by scatter diagram.
e. Correlation coefficient (r) lies between -1 and +1.
- Negative r = Negative correlation (as one variable increase, another variable decreases)
- Positive r = Positive correlation (as on variable increase, another variable also increases)
- 0 < r < 0.3 = Weak positive correlation
- 0.3 <r < 0.7 = Moderate positive correlation
- r > 0.7 = Strong positive correlation
f. Coefficient of determination = r² (0 to 1); percentation of variation in one variable that can be explained by variation in another variable
g. If we have a regression equation Y = 0.3X1 + 4X2, then the regression coefficient of X1 is 0.3 and the regression coefficient of X2 is 4.This means that when X1 increases by 1 unit, Y will increase by 0.3Also, when X2 increases by 1 unit, Y will increase by 4 units.