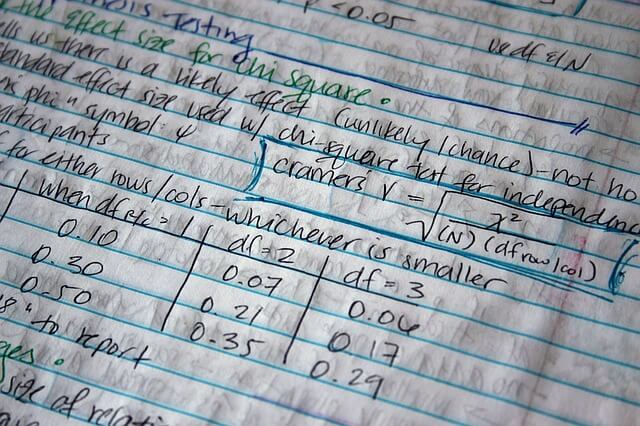Statistics – High Yield (Cheat Sheet)

Normal distribution

• Mean = Median = Mode
• 1 SD mean = 68.3% values
• 2 SD mean = 95.4% values
• 3 SD mean = 99.7% values
• Mean +/- 1.96 SD = 95% confidence interval
• SD = Square root (variance)

Non-normal distribution

a. Positive skew: Longer or fatter tail on right

• Mean > Median > Mode

b. Negative skew: Longer or fatter tail on left

• Mode > Median > Mean

2X2 tables

	Disease present	Disease absent
Test positive	TP	FP
Test negative	FN	TN

	Event	Non-event
Exposed or Treatment	a	b
Non-exposed or Placebo	c	d

Formulae

Incidence = No. of new cases in a given time/Total population at risk

Prevalence = No. of existing cases/Total population

Prevalence = Incidence X Duration

Case fatality rate = No. of death from a disease in given time/No. of cases in a given time

Sensitivity = True positive/Disease positive = TP/(TP+FN)

• Most acceptable screening tests are >80% sensitive

Specificity = True negative/Disease negative = TN/(TN+FP)

• Most acceptable confirmatory tests are >85% specific

False negative (FN) = 1 – Sensitivity

False positive (FP) = 1 – Specificity

Positive predictive value (PPV) = True positive/Test positive = TP/(TP + FP)

• Prevalence dependent (high prevalence = high PPV)

Negative predictive value (NPV) = True negative/Test negative = TN/(TN + FN)

• Prevalence dependent (low prevalence = high NPV)

Accuracy = (TP + TN)/(TP + FP + FN + TN)

Positive likelihood ratio = TP rate/FP rate = Sensitivity/(1-Specificity)

• Prevalence independent

Negative likelihood ratio = FN rate/TP rate = (1-Sensitivity)/Specificity

• Prevalence independent

Odds = Probability/(1-Probability)

Probability = Odds/(Odds + 1)

Pretest probability = Prevalence

Pretest odds = Pretest probability/(1-Pretest probability)

Post-test odds = Pre-test odds X Likelihood ratio

Post-test probability = Post-test odds/(1 + Post-test odds)

Posttest probability of positive test = PPV

Posttest probability of negative test = 1 – NPV

Relative risk (RR) = Experimental event rate/Control event rate = EER/CER = a/(a+b)/c/(c+d)

• Cohort study
• RR >1 = positive relationship between exposure and disease
• RR <1 = negative relationship between exposure and disease
• RR 1 = no relationship between exposure and disease

Attributable risk (AR) or Absolute risk reduction (ARR) = EER – CER = a/(a+b)/c/(c+d)

• AR = Rate of disease in exposed – Rate of disease in non-exposed
• ARR = Rate of disease in control group – Rate of disease in intervention group

Relative risk reduction = ARR/CER = (EER – CER)/CER

Numbers needed to treat (NNT) = 1/ARR

Numbers needed to harm (NNH) = 1/AR

Odds ratio = Odds of exposure in cases/Odds of exposure in controls = a/c/b/d = ad/bc

• Case-control study

Significance tests

Null hypothesis (H0) = No association exists between 2 selected variables (no difference between 2 treatments)

Alternate hypothesis (H1) = Association exists between 2 selected variables (difference exists between 2 treatments)

Type I error: Null hypothesis is rejected even though it is true (false positive)

• Not affected by sample size
• Increased if the number of end-points are increased

Type II error: Null hypothesis is not rejected even though it is false (false negative)

• Determined by both sample size and alpha

P-value (alpha): Probability of type I error

• Equals the significance level of a test
• If p <0.05, null hypothesis can be rejected (significant relationship exists between groups)

Beta: Probability of type II error

Power: 1 – Beta (i.e. probability of rejecting null hypothesis when it is false)

• Usually power of 0.8 is selected
• Increased sample size = Increased power
• Increased power = Decreased probability of type II error

Analyzing data

Which statistical test to use?

See more